matura maturzysta: zadanie z matury rozszerzonej zad 7 Punkt A = (−2,5) jest jednym z wierzchołków trójkąta równoramiennego ABC, w którym | AC |=| BC | . Pole tego trójkąta jest równe 15. Bok BC jest zawarty w prostej o równaniu y = x +1. Oblicz współrzędne wierzchołka C.

maturzysta:

maturzysta: odp z nata C(3,5 : 4,5) lub C( −1,5 : −0,5) mi wyszło C( 5, 6) lub C( −3, −2)

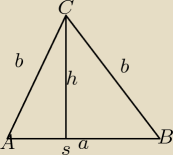
robinka: ja bym się za to w ten sposób zabrała B=(x,x+1)

	x−2		x+1+5		x−2		x+6
S=(		,		)=(		,		)
	2		2		2		2

|AB|=√(x+2)²+(x−4)² |CS|=√(^x−2₂−x)²+(^x+6₂−x−1)²

	1
P=		|AB|*|CS|
	2

	1
15=		*√(x+2)2+(x−4)2*√(x−22−x)2+(x+62−x−1)2
	2

maturzysta: ile to wychodzi

maxiol77: dobrze ci wysz lo mi tyle samo

arti: kurde robilem tak jak robinka ale mi sie nie chcialo tego wyliczac

maturzystka: zaraz wam tu napisze rozwiazanie

maturzystka: y = x + 1 ⊥ y = −3 + b A (−2,5) 5= 2+b b= 3 y = −x +3 punkt przecięcia: z układu równań obliczamy wychodzi S = (1,2) h = |SA|= √3²+3² = 3√2 P=15 więc P=ah/2 15 = a3√2/2 a=5√2 ¹₂a= ^5√2₂ (x−a)²+(y−b)²=r² S = (1,2) (x−1)²+(y−2)²=²⁵₂ O teraz to rownanie okregu oraz y = x +1 traktujemy jako układ równań w końcu wychodzą odpowiedzi takie jak te podane przez was

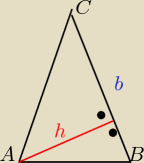
suseł: h_b= d −−− odległość A(−2,5) od prostej BC: x−y+1=0

	| −2−5 +1|
hb=		= U{6}{√2= 3√2
	√1+1

P(ΔABC) = ¹₂*b*h_b ¹₂*b*3√2 => b= 5√2 okrąg o srodku w A i r= b przecina prostą y= x+1 w punkcie szukanym C r²= (5√2)²= 50 o: ( x+2)² +( y−5)²= 50 i prosta y= x+1 x²+4x +4 +( x−4)² =50 x² +4x +4 +x² −8x +16 −50=0 2x² −4x −30=0 x²−2x −15=0 Δ= 64 √Δ= 8 x₁= 5 v x₂= −3 to: y₁= 5+1= 6 v y₂= −3+1= −2 są dwa takie punkty spełniajace warunki zad. C₁( 5,6) C₂( −3, −2) w/g mnie to jest poprawna odpowiedź

suseł: Basia możesz "luknąć"

Godzio: sprytnie

Basia: Tak samo robiłam i wynik mam taki sam. No to chyba dobrze. Na Interii są już nieoficjalne rozwiązania. Nie wiem jak na OKE Poznań, arkusze na pewno są, ale czy rozwiązania nie sprawdzałam.

suseł: Pytam , bo "młodzi" podają też inne rozwiązania

suseł: Basiu Jak oceniasz stopień trudności zadań na rozszerzonej oczywiście, bo na podstawie to naprawdę łatwiutkie , aż za bardzo Nie ma to jak Nasze dawne,...... prawdziwe matury z matematyki Uważam ,że na rozszerzeniu zadania były dość proste, spodziewałam się o wiele trudniejszych.

Basia: Moim zdaniem 1−9 łatwe. Nawet zbyt łatwe jak na poziom rozszerzony. 10 wprawdzie nie trudne, ale żmudne. Naprawdę trudne jest 11. Już je tu kiedyś na forum rozwiązywałam, ale ograniczyłam się do podania schematu rozwiązania, bo liczyć mi się tego nie chciało. Teraz też mi się nie chce. Też spodziewałam się trudniejszych, przede wszystkim mniej schematycznych i wymagających nie tylko "rachunków", ale także pomysłu. Biorąc jednak pod uwagę fakt, że to tylko 3 godziny, to można chyba uznać, że należało się jednak sporą wiedzą i sprawnością wykazać. A podstawa to..............

Basia: Jeśli chodzi o 7, to na Interii takie same wyniki. Rozwiązania w całości nie ma.

Basia: Jakaś "zdechnięta" dzisiaj jestem. Chyba pogoda mnie dobija, bo leje jak z cebra. Na dodatek ziąb, teraz około 8 stopni. I to ma być maj ! Protestuję. Młodzież poszła spać, bo przecież jutro język obcy zdają, to i na mnie chyba pora. Dobranoc

Tomek.Noah: Wg mnie bardzo pomyslowe rozwiazanie nie wpadlbym na taki ale naszczescie mature z matmy mam za rok robilem spr. waszej metody i wychodzi ze |AC|=|AB| a powinno byc |AC|=|BC|

Pawel: Marura nie była trudna to fakt, pierwsze zadania to takie schematy ze sodoma,ale jak dla mnie za duzo było w stylu udowodnij a nie cierpnie takich.